En statistiques descriptives, un diagramme en boîte ou boxplot (également connu sous le nom de diagramme en boîte et de diagramme à moustaches) est un type de graphique souvent utilisé dans l’analyse de données explicatives. Les diagrammes en boîte montrent visuellement la distribution des données numériques et l’asymétrie en affichant les quartiles (ou percentiles) et les moyennes des données.
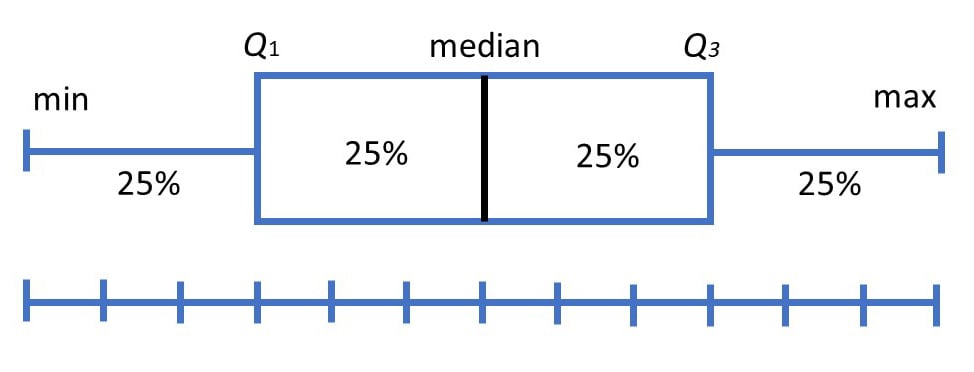
Les diagrammes en boîte montrent le résumé en cinq nombres d’un ensemble de données : le score minimum, le premier quartile (inférieur), la médiane, le troisième quartile (supérieur) et le score maximum.
CHAPITRES
ToggleDéfinitions
Score minimum
Le score le plus bas, à l’exclusion des valeurs aberrantes (indiquées à l’extrémité de la moustache gauche).
Quartile inférieur
Vingt-cinq pour cent des scores sont inférieurs à la valeur du quartile inférieur (également appelé premier quartile).
Médiane
La médiane marque le point médian des données et est représentée par la ligne qui divise la boîte en deux parties (parfois appelée deuxième quartile). La moitié des scores est supérieure ou égale à cette valeur, et l’autre moitié est inférieure.
Quartile supérieur
Soixante-quinze pour cent des scores se situent en dessous de la valeur du quartile supérieur (également appelé troisième quartile). Ainsi, 25 % des données sont supérieures à cette valeur.
Score maximal
Le score le plus élevé, à l’exclusion des valeurs aberrantes (indiquées à l’extrémité de la moustache de droite).
Moustaches
Les moustaches supérieures et inférieures représentent les scores en dehors des 50% du milieu (c’est-à-dire, l’intervalle interquartile (ou IQR)
Le diagramme en boîte montre la moitié moyenne des scores (c’est-à-dire l’intervalle entre le 25e et le 75e rang), l’intervalle entre le 25e et le 75e percentile).



Pourquoi les diagrammes en boîte sont-ils utiles ?
Les diagrammes en boîte divisent les données en sections contenant environ 25 % des données de cet ensemble.
Les diagrammes en boîte sont utiles car ils fournissent un résumé visuel des données permettant aux chercheurs d’identifier rapidement les valeurs moyennes, la dispersion de l’ensemble de données et les signes d’asymétrie.
Notez que l’image ci-dessus représente des données qui sont une distribution normale parfaite et que la plupart des diagrammes en boîte ne se conforment pas à cette symétrie (où chaque quartile est de la même longueur).
Les diagrammes en boîte sont utiles car ils montrent le score moyen d’un ensemble de données
La médiane est la valeur moyenne d’un ensemble de données et est représentée par la ligne qui divise la boîte en deux parties. La moitié des résultats est supérieure ou égale à cette valeur, et l’autre moitié est inférieure.
Les diagrammes en boîte sont utiles car ils montrent l’asymétrie d’un ensemble de données
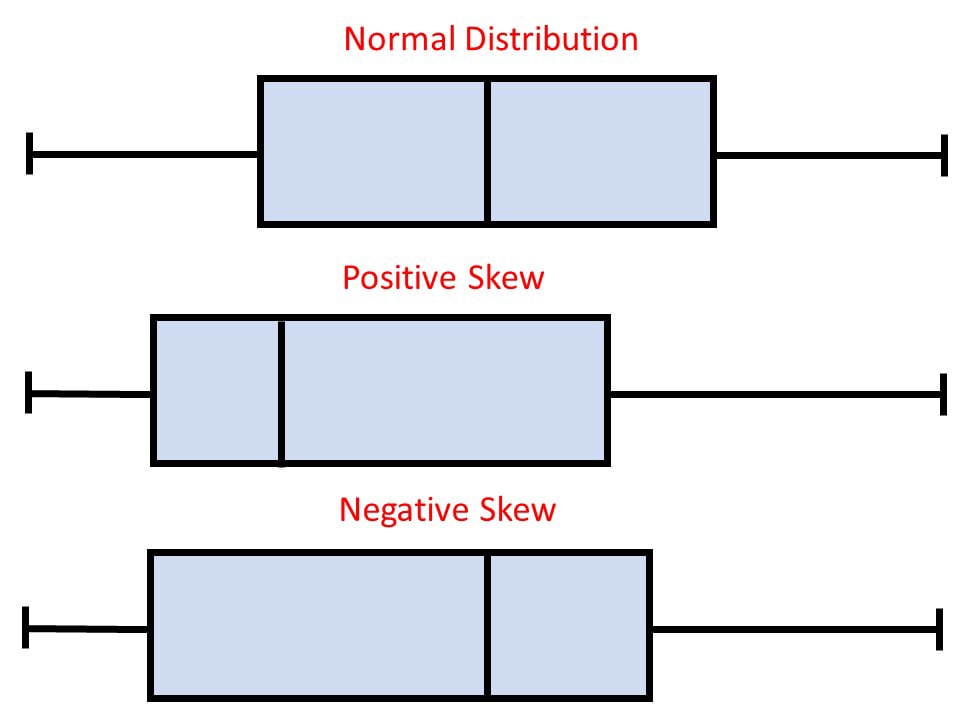
La forme du diagramme en boîte montre si un ensemble de données statistiques est normalement distribué ou asymétrique.
Lorsque la médiane se trouve au milieu de la boîte et que les moustaches sont à peu près les mêmes des deux côtés de la boîte, la distribution est symétrique.
Lorsque la médiane est plus proche du bas de la boîte et que la moustache est plus courte à l’extrémité inférieure de la boîte, la distribution est positivement asymétrique (à droite).
Lorsque la médiane est plus proche du haut de la boîte et que la moustache est plus courte à l’extrémité supérieure de la boîte, la distribution est négativement asymétrique (à gauche).
Les diagrammes en boîte sont utiles car ils montrent la dispersion d’un ensemble de données
En statistique, la dispersion (également appelée variabilité, dispersion ou étalement) est la mesure dans laquelle une distribution est étirée ou comprimée.
Les valeurs les plus petites et les plus grandes se trouvent à l’extrémité des « moustaches » et sont utiles pour fournir un indicateur visuel de la dispersion des résultats (par exemple, l’étendue), l’intervalle).
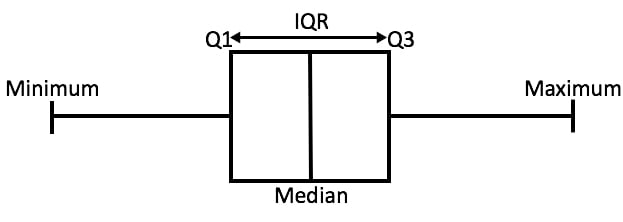
L’intervalle interquartile (IQR) est le diagramme en boîte montrant la moitié centrale des scores et peut être calculé en soustrayant le quartile inférieur du quartile supérieur (par exemple, Q3-Q1).
Les diagrammes en boîte sont utiles car ils montrent les valeurs aberrantes au sein d’un ensemble de données
Une valeur aberrante est une observation qui est numériquement éloignée du reste des données.
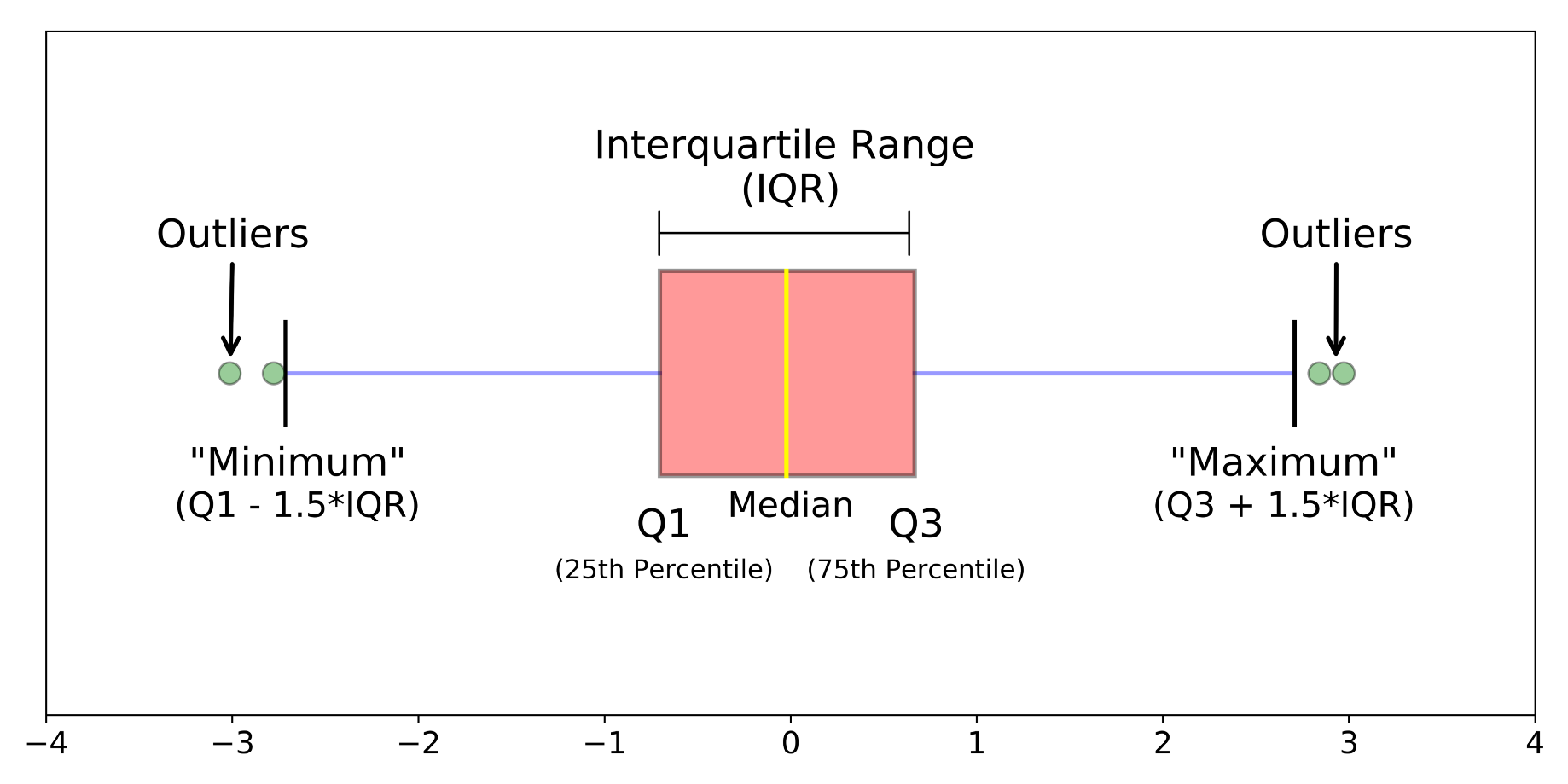
Lors de l’examen d’un diagramme en boîte, une valeur aberrante est définie comme un point de données situé en dehors des moustaches du diagramme en boîte.
Source : https://towardsdatascience.com/understanding-boxplots-5e2df7bcbd51
Par exemple, en dehors de 1.5 fois l’écart interquartile au-dessus du quartile supérieur et au-dessous du quartile inférieur (Q1 – 1,5 * IQR ou Q3 + 1,5 * IQR).
Comment comparer les diagrammes en boîte
Les diagrammes en boîte sont un moyen utile de visualiser les différences entre différents échantillons ou groupes. Ils permettent de fournir de nombreuses informations statistiques, notamment les médianes, les intervalles et les valeurs aberrantes.
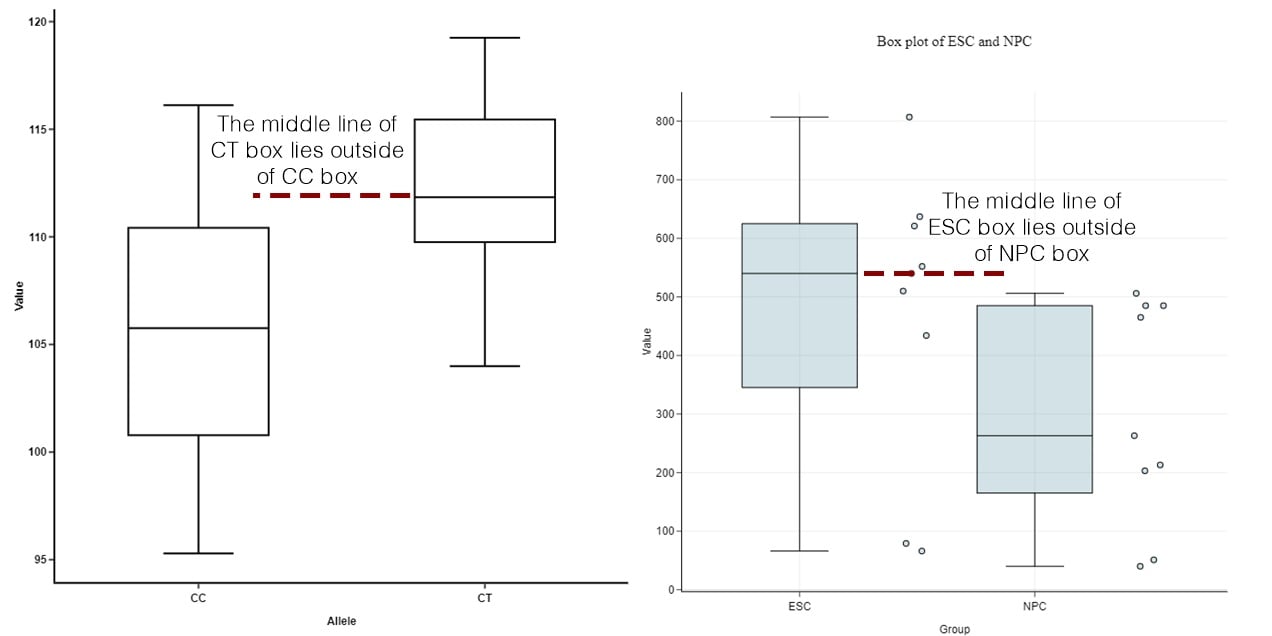
Étape 1 : Comparer les médianes des diagrammes en boîte
Comparer les médianes respectives de chaque diagramme en boîte. Si la ligne médiane d’un diagramme en boîte se situe en dehors de la boîte d’un diagramme en boîte de comparaison, il est probable qu’il y ait une différence entre les deux groupes.
Source : https://blog.bioturing.com/2018/05/22/how-to-compare-box-plots/
Étape 2 : Comparer les intervalles interquartiles et les moustaches des diagrammes en boîte
Comparer les intervalles interquartiles (c’est-à-dire les longueurs des boîtes) pour examiner la façon dont les données sont dispersées entre chaque échantillon. Plus la boîte est longue, plus les données sont dispersées. Plus elle est petite, moins les données sont dispersées.
Par la suite, regardez l’étendue globale, comme le montrent les valeurs extrêmes à l’extrémité de deux moustaches. Cela montre l’étendue des résultats (un autre type de dispersion). Des fourchettes plus grandes indiquent une distribution plus large, c’est-à-dire des données plus dispersées.
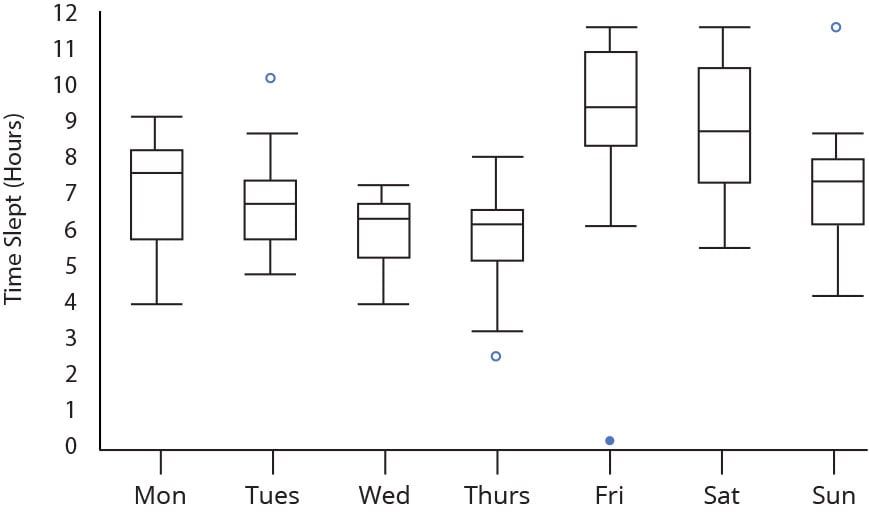
Étape 3 : Recherchez les valeurs aberrantes potentielles (voir l’image ci-dessus)
Lors de l’examen d’un diagramme en boîte, une valeur aberrante est définie comme un point de données situé à l’extérieur des moustaches du diagramme en boîte.
Étape 4 : Recherchez des signes d’asymétrie
Si les données ne semblent pas symétriques, chaque échantillon présente-t-il le même type d’asymétrie ?